Embeddings – numerical features of categorical data

In machine learning, the first step to train a model is to prepare data and features. If the dataset is tabular then the task in most cases can be done using statistical tests and wrapper methods to determine which features contribute to predicting our class the most. We can use them for both numerical or categorical data. Categorical data, we need to first encode as numerical, for instance using label or one-hot encoding. More interesting problem is when we need to encode categorical data that have relationships between elements in a sequence. Examples are words in sentences, amino acids in proteins, a sequence of products sold in a market etc. In each of these applications scientists and engineers may seek to predict what item comes next. This information can be encoded as a vector of features called embedding. The concept of an embedding as a vector of features of an element has a long and parallel history among others in machine learning, graph theory and dynamical systems, but has been popularized during Large Language Model (LLM) development. Please note that one-hot encoding also generate a vector for each category, therefore it is sometimes referred to as a traditional or conventional embedding technique.

Types of embeddings

We can distinguish the following types of embeddings:

• Frequency word embedding – in this approach, vector is generated using word frequencies. Exemplary approaches include TF-IDF and co-occurrence matrix.
• Static word embedding – these vectors have constant size and can be generated using neural networks. In this approach, a single word have a single vector assigned. Example of this category is word2vec.
• Contextual word embedding – in comparison to static word embedding, a single word may have multiple embeddings which are selected depending on a context.
• Sentiment aware embedding – it is able to distinguish two opposite words used in the same context. For instance, cold and hot which contextual and static word embeddings consider as similar.

word2vec architecture

One of the earliest method to generate static word embedding is word2vec. In this approach, a single word has a single vector assigned regardless whether it has multiple meanings. They can be trained using neural networks. The architecture for word2vec is shown in the figure below.

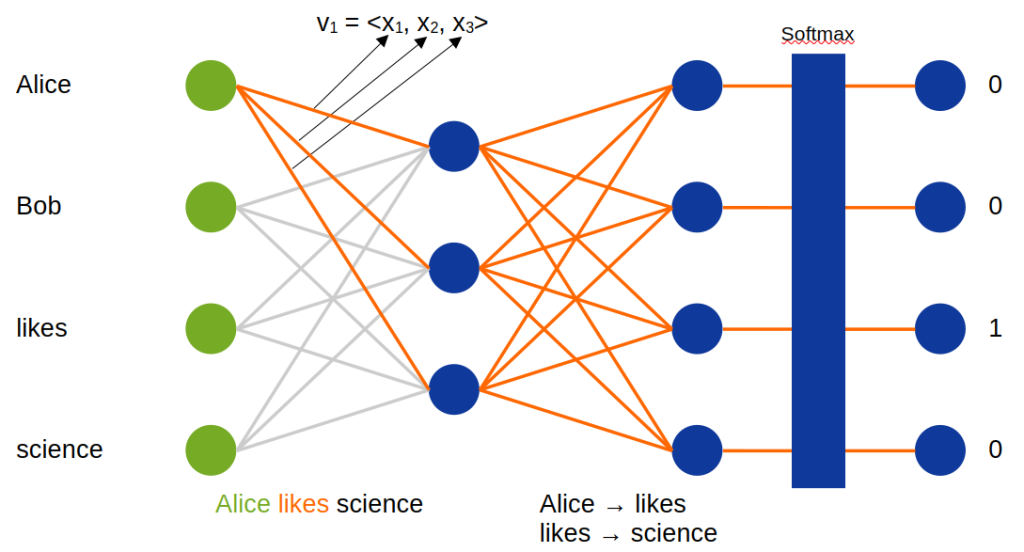
It consists of an input layer, embedding layer consisting of weights and linear activation (transfer) function, output layer with rectifier activation function, and softmax layer. Actually, embedding layer is simply a linear layer where weights connecting a single input with hidden layer are embedding values for a given word. In the figure , weights creating the embedding for word “Alice” are highlighted.

If we want to create embeddings for predicting a next word when typing on a screen keyboard, then from input text, we need to create pairs of words. The first word from a pair is the input and the second is the output. In the example above, we have two pairs, that are alice → likes and likes → science. For the first pair, we set the input vector in a way that word “alice” has value 1 and the rest have value 0 (one-hot encoding). Then, output we set in the same way, but we set value 1 next to the second word from the pair. Finally, we can calculate forwardpass and backpropagate the error, so adjust weights’ values.

Implementation

In PyTorch, a neural network used to create word embeddings can be implemented as below:

import io

import torch
import torch.nn as nn
from torch.nn import CrossEntropyLoss
from torch.utils.data import Dataset
from torch.utils.data import DataLoader
import torch.optim.lr_scheduler as lr_scheduler
from scipy.spatial import distance_matrix
import numpy as np
import pandas as pd


class W2vEmbedding(nn.Module):
    def __init__(self, *args, **kwargs):
        super().__init__(*args, **kwargs)

        self.embedding_size = 3
        self.alphabet_size = 4

        self.embedding = nn.Embedding(self.alphabet_size,self.embedding_size)  # Embedding layer
        self.hidden = nn.Linear(self.embedding_size,self.alphabet_size, bias=False)  # Output layer

    def forward(self, x):
        x = self.embedding(x)
        x = self.hidden(x)
        return x


def training_step(model, criterion, batch, batch_idx):
    input_i, label_i = batch
    output_i = model(input_i)
    torch.set_printoptions(threshold=10_000)
    loss = criterion(output_i.squeeze(1), label_i)
    return loss


def fit(model, data_loader):
    epochs = 100
    optimizer = torch.optim.Adam(model.parameters(), lr=0.1)
    criterion = CrossEntropyLoss()
    scheduler = lr_scheduler.LinearLR(optimizer, start_factor=1.0, end_factor=0.01, total_iters=max(10, epochs - 10))
    for epoch in range(epochs):
        losses = []
        for batch in data_loader:
            loss = training_step(model, criterion, batch, None)
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()
            losses.append(loss)
        previous_lr = optimizer.param_groups[0]["lr"]
        scheduler.step()
        current_lr = optimizer.param_groups[0]["lr"]
        print(f"epoch: {epoch}, previous_lr: {previous_lr}, current_lr: {current_lr}")


class W2vDataset(Dataset):

    def __init__(self):
        self.words = torch.Tensor([
            0,  # Alice
            1,  # Bob
            2,  # likes
            2,  # likes
            2,  # likes
        ]).int()
        self.labels = torch.Tensor([
            [0, 0, 1, 0],  # likes
            [0, 0, 1, 0],  # likes
            [0, 0, 0, 1],  # science
            [1, 0, 0, 0],  # Alice
            [0, 1, 0, 0],  # Bob
        ])

    def __getitem__(self, idx):
        return self.words[idx], self.labels[idx]
        
    def __len__(self):
        return len(self.labels)


def dist_matrix(embeddings):
    words = ["Alice", "Bob", "likes", "science"]
    embeddings = embeddings.detach().cpu().numpy()
    dist = distance_matrix(embeddings, embeddings, 2)
    dist = (dist - dist.min()) / (dist.max() - dist.min())
    data = np.column_stack((dist.round(4), words))
    df = pd.DataFrame(data, columns=words + ['WORDS'])
    return df


ds = W2vDataset()
data_loader = DataLoader(ds, batch_size=1)
embedding_model = W2vEmbedding()
fit(embedding_model, data_loader)
for name, param in embedding_model.named_parameters():
    if name == "embedding.weight":
        df = dist_matrix(param)
        print(f"{name}: {param}")
        print()
        print(df)

Note that in this code, we used Embedding layer, Linear layer and CrossEntropyLoss which already uses softmax. The code above, trains four embeddings with three values each. Exemplary output is shown below:

embedding.weight: Parameter containing:
tensor([[ 0.1777, -2.6689, -0.2689],
        [ 0.0172, -2.7118,  0.2326],
        [-0.1374,  1.5212,  0.4373],
        [-2.7651,  1.3725, -0.2458]], requires_grad=True)

    Alice     Bob   likes science    WORDS
0     0.0  0.1057  0.8523     1.0    Alice
1  0.1057     0.0  0.8483  0.9931      Bob
2  0.8523  0.8483     0.0  0.5439    likes
3     1.0  0.9931  0.5439     0.0  science

We can see that the first two vectors are close to each other in comparison to the rest. This is because they are used in the same context.

Summary

Embeddings are compressed representation of categorical features queued in a sequence and they represent relationship between them. We already have many different approaches to word embeddings aiming at represent different relationships between elements.